맨위로가기

요한 하인리히 람베르트

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

요한 하인리히 람베르트는 1728년 뮐루즈(현재 프랑스 알자스)에서 태어난 스위스-독일의 수학자, 물리학자, 천문학자, 철학자이다. 그는 12세에 학교를 그만두고 독학으로 공부하며 개인 교사, 편집자 비서 등 다양한 직업을 거쳤다. 1763년 프로이센 과학 아카데미의 직책을 제안받아 프리드리히 2세의 후원을 받았고, 오일러와 교류하며 활발한 연구 활동을 펼쳤다. 람베르트는 원주율의 무리수임을 증명하고, 비유클리드 기하학에 대한 아이디어를 제시했으며, 지도 투영법, 측광학, 습도계 등 다양한 분야에서 업적을 남겼다. 또한, 람베르트-베르의 법칙을 소개하고, 우주론, 삼단논법 연구에도 기여했다.

더 읽어볼만한 페이지

  • 스위스의 논픽션 작가 - 막스 피카르트
    막스 피카르트는 독일 출신의 스위스 철학자이자 작가로, 현대 문명을 비판하고 침묵의 가치를 강조하며 인간 내면의 폭력성을 탐구하고 가톨릭으로 개종했다.
  • 스위스의 천문학자 - 디디에 쿠엘로
    디디에 쿠엘로는 스위스의 천문학자로, 미셸 마요르와 함께 51 페가수스 b를 발견하여 2019년 노벨 물리학상을 공동 수상하였으며 외계 행성 탐색 및 특성 분석에 기여했다.
  • 스위스의 천문학자 - 프리츠 츠비키
    프리츠 츠비키는 초신성, 중성자별, 암흑 물질 등을 연구하고 은하 목록을 작성했으며, 형태학적 분석 기법을 개발하여 1972년 영국 왕립 천문학회 금메달을 수상한 스위스계 미국인 천문학자이다.
  • 요한 하인리히 람베르트 - 비어-람베르트 법칙
    비어-람베르트 법칙은 빛이 물질을 통과할 때 빛의 세기가 감소하는 정도를 설명하는 법칙으로, 흡광도는 물질의 농도와 빛이 통과하는 거리에 비례한다는 것을 나타내며, 다양한 분야에서 활용된다.
  • 요한 하인리히 람베르트 - 람베르트 W 함수
    람베르트 W 함수는 we^w = z를 만족하는 w를 찾는 람베르트 이름을 딴 역함수 관계를 가지며, 여러 분야에서 지수 함수 방정식을 푸는 데 응용되는 무한히 많은 가지를 가진 함수이다.
요한 하인리히 람베르트 - [인물]에 관한 문서
기본 정보
이름요한 하인리히 람베르트
원어 이름Johann Heinrich Lambert
Jean-Henri Lambert
출생일1728년 8월 26일 또는 28일
출생지뮐루즈 공화국 (현재 프랑스 알자스)
사망일1777년 9월 25일
사망지프로이센 왕국 베를린
국적뮐루즈 공화국
스위스
프랑스
분야수학
물리학
천문학
철학
학문적 정보
알려진 업적원주율이 무리수임을 처음으로 증명
베르-람베르트 법칙
람베르트 코사인 법칙
횡단 메르카토르 도법
람베르트 W 함수
이미지
요한 하인리히 람베르트 (1728–1777)
서명
람베르트 서명
람베르트 서명

2. 생애

람베르는 1728년 당시 스위스와 동맹을 맺은 도시 국가였던 뮐루즈[4](현재 알자스, 프랑스 소속)에서 위그노 가정에서 태어났다.[1] 출생일은 8월 26일이라는 자료와 8월 28일이라는 자료가 있다.[2][3][4] 12세에 학교를 그만둔 그는 여러 직업을 전전하면서도 여가 시간을 이용해 계속 공부했다. 그의 직업에는 아버지(재봉사)의 조수, 근처 제철소의 사무원, 개인 교사, 바젤 차이퉁 편집자의 비서, 그리고 20세에는 쿠어에 있는 칼리스 백작의 아들들을 위한 개인 교사가 포함된다. 1756년부터 1758년까지 제자들과 함께 유럽을 여행하면서 독일 여러 주, 네덜란드, 프랑스, 이탈리아 여러 주의 저명한 수학자들을 만났다. 쿠어로 돌아온 그는 광학과 우주론에 관한 첫 번째 책을 출판하고 학문적인 직책을 얻으려고 노력했다. 몇몇 단기적인 직책을 거친 후, 그는 1763년 베를린의 프로이센 과학 아카데미의 직책 제안을 받았고, 프리드리히 2세의 후원을 받게 되어 오일러와 친구가 되었다. 이 자극적이고 경제적으로 안정적인 환경에서 그는 1777년 사망할 때까지 왕성하게 활동했다.[4]

2. 1. 초기 생애와 교육

요한 하인리히 람베르트는 1728년 당시 스위스와 동맹을 맺은 도시 국가였던 뮐루즈(현재 프랑스 알자스)에서 위그노 가정에서 태어났다.[4][1] 출생일은 8월 26일이라는 자료와 8월 28일이라는 자료가 있다.[2][3][4]

12세에 학교를 그만둔 그는 아버지(재봉사)의 조수, 근처 제철소의 사무원, 개인 교사, 바젤 차이퉁 편집자의 비서등의 여러 직업을 전전하면서도 여가 시간을 이용해 계속 독학으로 공부했다.[4] 20세에는 쿠어에 있는 칼리스 백작 가문의 가정교사가 되었다.[4] 1756년부터 1758년까지 제자들과 함께 유럽을 여행하면서 독일 여러 주, 네덜란드, 프랑스, 이탈리아 여러 주의 저명한 수학자들을 만났다.[4]

2. 2. 베를린 시기

람베르트는 1763년 프로이센 과학 아카데미의 직책 제안을 받고 프리드리히 2세의 후원을 받으며 오일러와 친구가 되었다.[4] 이 시기 람베르트는 경제적으로 안정적인 환경에서 1777년 사망할 때까지 왕성하게 연구 활동을 했다.[4]

3. 주요 업적

3. 1. 수학

1763년 《악타 에루디토룸》(Acta Eruditorum)에 실린 그림


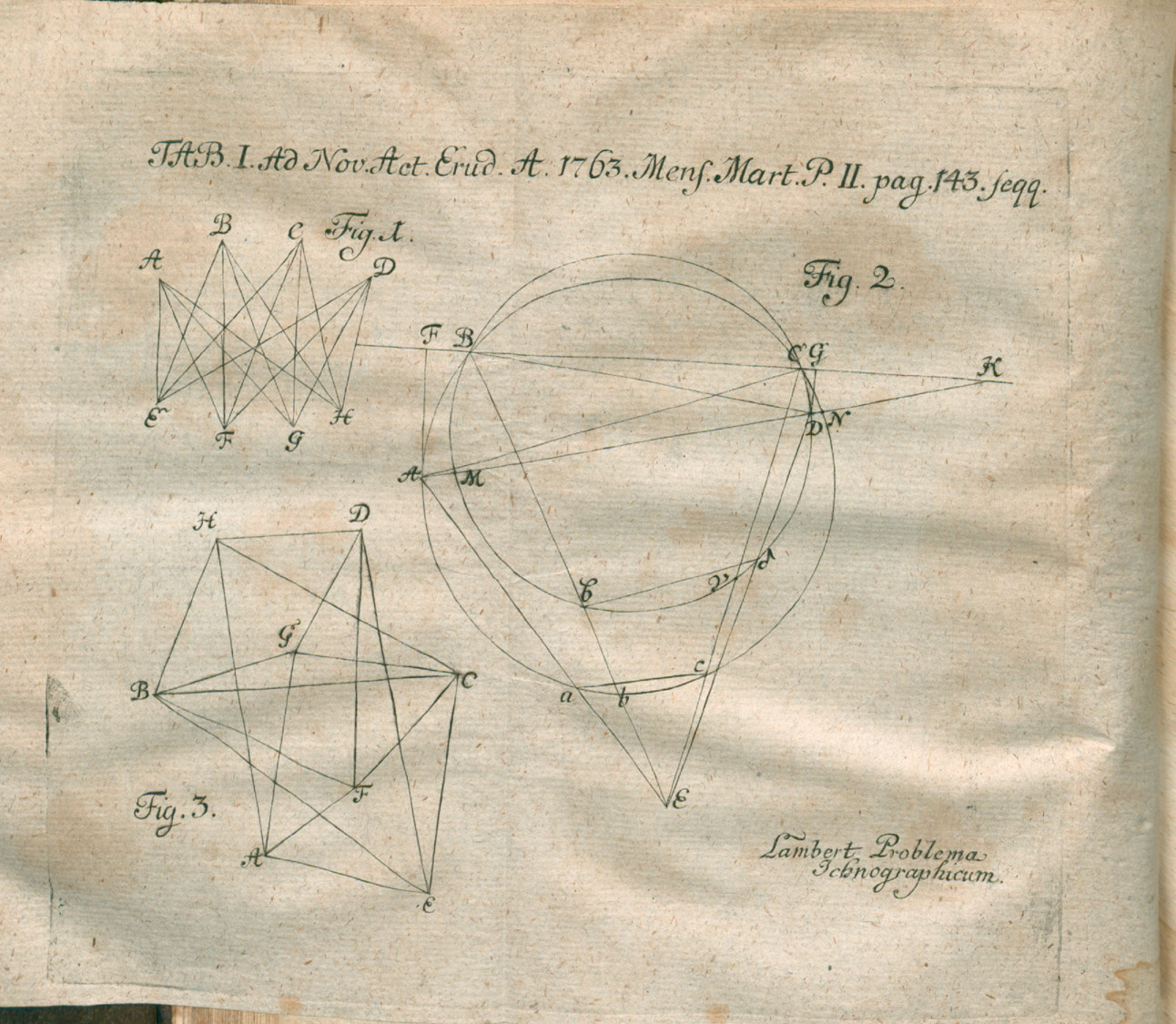
람베르트는 최초로 삼각법에 쌍곡선 함수를 도입했다.[5] 또한 비유클리드 기하학 공간에 대한 추측을 제기했으며, 함수 tan x에 대한 일반화 연분수를 사용하여 π가 무리수임을 증명한 최초의 증명을 한 것으로 인정받는다.[5] 람베르트는 원뿔곡선에 대한 정리를 고안하여 혜성의 궤도 계산을 단순화하기도 했다.

람베르트는 각과 쌍곡선 삼각형의 면적 사이의 관계에 대한 공식을 고안했다. 이 삼각형들은 평평한 유클리드 면 대신 안장과 같이 오목한 면에 그려진 삼각형이다. 람베르트는 각의 합이 π(라디안) 또는 180° 미만임을 보였다. 결손(부족량)은 면적에 따라 증가한다. 즉, 쌍곡선 삼각형의 면적(상수 C를 곱한)은 π(라디안) 또는 180°에서 각 α, β, γ의 합을 뺀 값과 같다. 여기서 C는 현재 의미에서 면의 곡률의 음수를 나타낸다. 삼각형이 커지거나 작아짐에 따라 각은 변하는데, 이는 닮은 삼각형의 존재를 금지한다. 왜냐하면 같은 각을 가진 삼각형만이 같은 면적을 가지기 때문이다. 따라서 유클리드 기하학에서처럼 삼각형의 면적이 변의 길이로 표현되는 대신 람베르트의 쌍곡선 삼각형의 면적은 각으로 표현될 수 있다.

1761년에는 원주율의 무리수임을 증명하였다.[27] 1766년에는 『평행선의 이론』[29]에서 비유클리드 기하학으로 이어지는 평행선 공준에 대한 생각을 밝혔다. 1772년에는 지도 투영법의 횡적 메르카토르 도법, 람베르트 정적 방위도법, 람베르트 정각 원추도법, 람베르트 정적 원통도법, 람베르트 정적 원추도법을 고안하였다.[30]

3. 2. 지도 투영법

람베르트는 구형 지구의 지도 투영법의 일반적인 특성을 다룬 최초의 수학자였다.[7] 특히 그는 각도를 보존하는 성질(등각성)과 면적을 보존하는 성질을 최초로 논의하고, 이 두 성질이 서로 배타적임을 지적했다.[8] 1772년, 람베르트는[9][10] '''Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten'''(Notes and Comments on the Composition of Terrestrial and Celestial Maps영어|왈도 토블러(1972)가 '''지구 및 천체 지도 제작에 대한 주석 및 추가 사항'''으로 번역)[11]라는 제목으로 7가지 새로운 지도 투영법을 발표했다.[30] 람베르트는 자신의 투영법에 이름을 붙이지 않았지만, 현재는 람베르트 정각 원뿔 투영, 가로 메르카토르 투영, 람베르트 등적 방위도법, 라그랑주 투영, 람베르트 등적 원통 투영, 가로 원통 등적 투영, 람베르트 등적 원뿔 투영으로 알려져 있다. 이 중 처음 세 가지는 매우 중요하다.[8][12]

3. 3. 물리학 (측광학)

람베르트는 최초의 실용적인 습도계를 발명했다.[31] 1760년, 그는 측광법(광학)에 관한 책인 ''측광법''을 출판하여 이 분야를 확립했다. 빛이 직선으로 진행한다는 가정에서 그는 조명이 광원의 세기에 비례하고, 조명된 표면까지의 거리의 제곱에 반비례하며, 빛의 방향과 표면의 방향 사이의 각도의 사인에 비례한다는 각도의 사인에 비례한다는 것을 보였다. 이러한 결과는 조명의 시각적 비교를 포함하는 실험에 의해 뒷받침되었으며, 조명 계산에 사용되었다. ''측광법''에서 람베르트는 피에르 부게르가 더 일찍 공식화한 빛 흡수 법칙(비어-람베르트 법칙)을 인용하고,[15][25][26] 알베도라는 용어를 도입했다.[16] 람베르트 반사는 그의 이름을 따서 명명되었다. 그는 투시에 관한 고전적인 저술을 남겼고, 기하 광학에도 기여했다. 휘도의 비SI 단위인 람베르트는 측광학 연구를 확립한 그의 업적을 기리는 명칭이다. 람베르트는 또한 3차원 색 모델 개발의 선구자였다. 늦은 나이에 그는 삼각형 색 피라미드("Farbenpyramide")에 대한 설명을 출판했는데, 이것은 빨강, 노랑, 파랑 안료를 다양하게 결합하고, 수직 성분을 제공하기 위해 흰색의 양을 증가시켜 6개의 다른 수준에 총 107가지 색상을 보여준다.[17] 그의 연구는 토비아스 마이어의 이전 이론적 제안을 기반으로 하여 이러한 초기 아이디어를 크게 확장했다.[18] 이 프로젝트에서 람베르트는 궁정 화가 벤자민 칼라우의 도움을 받았다.[19]

3. 4. 철학

람베르트는 주요 철학 저서인 『노이에스 오르가논/Neues Organonde』(1764, 아리스토텔레스의 『오르가논/Ὄργανονgrc』에서 이름을 따옴)에서 주관적인 외양과 객관적인 외양을 구분하는 규칙을 연구하여 자신의 광학 연구와 연결시켰다. 『노이에스 오르가논』에는 '현상학(phenomenology)'이라는 용어가 처음 등장한 것 중 하나가 포함되어 있으며, 다양한 삼단논법의 종류를 제시하고 있다. 존 스튜어트 밀에 따르면, 람베르트는 『노이에스 오르가논』에서 가장 정교하고 완전한 삼단논법적 학설 해설 중 하나를 담고 있으며, 어떤 종류의 논증이 네 가지 그림 중 각각에 가장 적합하고 자연스럽게 들어맞는지 명시적으로 조사했고, 그의 조사는 매우 독창적이고 명료한 사고를 특징으로 한다.[21] 『노이에스 오르가논』의 현대판은 1990년 베를린 아카데미-페어라그(Akademie-Verlag)에서 출판되었다.

1765년 람베르트는 임마누엘 칸트와 서신을 교환하기 시작했다. 칸트는 『순수이성비판(Critique of Pure Reason)을 람베르트에게 헌정할 의도였지만, 작업이 지연되어 람베르트 사후에 출판되었다.[22]

3. 5. 천문학

람베르트는 토머스 라이트와 이마누엘 칸트가 독립적으로 개발한 성운설과 유사한 우주 생성 이론을 발전시켰다. 라이트와 칸트의 발표 직후, 람베르트는 태양계의 기원에 대한 성운설을 자신의 버전으로 "우주 건설의 설비에 관한 우주론적 편지" (''Cosmologische Briefe über die Einrichtung des Weltbaues'') (1761)에 발표했다. 람베르트는 태양 근처의 별들이 은하수를 통해 함께 이동하는 집단의 일부이며, 은하 전체에 걸쳐 이러한 집단 (별계)들이 많이 있다고 가정했다. 이는 훗날 윌리엄 허셜 경에 의해 확인되었다. 그는 또한 천체역학에서 궤도의 일부를 따라 비행 시간을 결정하는 문제인 람베르트 문제를 해결했다. 이 분야에서 그의 업적은 그의 이름을 딴 소행성 187 람베르타에 기념되었다.

3. 6. 기상학

람베르트는 주기적 현상을 관측하고 그 법칙을 유도하여 점진적으로 이론을 확장하는 방법을 기상학 연구에 적용해야 한다고 주장했다. 그는 기상학을 더 과학적으로 만들기 위해서는 천문학자들처럼 일반 법칙과 중간 운동을 먼저 확립해야 한다고 보았다.[23]

람베르트는 "기상학에도 일반 법칙이 있고 많은 수의 주기적 현상이 포함되어 있다는 것은 확실한 사실"이라며, "지금까지는 몇 가지 관측만 이루어졌고, 이들 사이에는 연관성을 찾을 수 없다"고 지적했다.[23]

더 많고 질 좋은 기상 데이터를 얻기 위해, 람베르트는 전 세계에 기상 관측소 네트워크를 구축하여 다양한 기상 상태(비, 구름, 건조 등)를 기록할 것을 제안했다. 이 방법은 오늘날에도 여전히 사용되고 있다.[23] 그는 또한 기상학 발전을 위해 측정 기기 개선과 정확한 개념 정립에 힘썼으며, 1769년과 1771년에는 습도 측정과 습도계에 관한 저서를 발표했다.[23]

4. 저서

참조

[1] 간행물 Mulhouse https://hls-dhs-dss.[...]
[2] 서적 The Bloomsbury Companion to Kant https://books.google[...] Bloomsbury Academic 2015-03-26
[3] 웹사이트 Johann Heinrich Lambert https://www.britanni[...] 2020-08-24
[4] 웹사이트 Johann Heinrich Lambert (1728–1777) http://www.maths.tcd[...] 1908
[5] 논문 Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques https://babel.hathit[...] 1761
[6] 서적 Indian Mathematics and Astronomy: Some Landmarks Jnana Deep Publications 1994
[7] 서적 Acta Eruditorum http://atena.beic.it[...] 1763
[8] 서적 Flattening the Earth: Two Thousand Years of Map Projections University of Chicago Press 1993
[9] 서적 Ammerkungen und Zusatze zurder Land und Himmelscharten Entwerfung 1772
[10] 서적 Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten (1772) https://archive.org/[...] W. Engelmann 2018-10-14
[11] 서적 Notes and Comments on the Composition of Terrestrial and Celestial Maps http://store.esri.co[...] University of Michigan Press 1972
[12] 서적 The Times Atlas of the World Houghton Mifflin 1967
[13] 논문 Map Projections - A Working Manual. U.S. Geological Survey Professional Paper 1395 https://pubs.er.usgs[...] United States Government Printing Office, Washington, D.C. 1987
[14] 웹사이트 Cylindrical Projections http://www.geo.hunte[...] City University of New York 2007-03-30
[15] 웹사이트 Pierre Bouguer | French scientist https://www.britanni[...]
[16] 서적 The Principles of Physical Optics Dover 2003
[17] 서적 Beschreibung einer mit dem Calauschen Wachse ausgemalten Farbenpyramide wo die Mischung jeder Farben aus Weiß und drey Grundfarben angeordnet, dargelegt und derselben Berechnung und vielfacher Gebrauch gewiesen wird 1772
[18] 서적 The Creation of Color in Eighteenth-Century Europe http://www.gutenberg[...] Columbia University Press 2006
[19] Translation of "Beschreibung einer mit dem Calauischen Wachse ausgemalten Farbenpyramide" ("Description of a colour pyramid painted with Calau's wax"), 1772, with an introduction by Rolf Kuehni Johann Heinrich Lambert's Farbenpyramide http://www.iscc.org/[...] 2011
[20] 서적 Preface of vol. I 1700
[21] 서적 A System of Logic https://archive.org/[...] 1843
[22] 서적 Revolutions of Geometry Wiley 2010
[23] 논문 Johann Heinrich Lambert's Scientific Tool Kit, Exemplified by His Measurement of Humidity, 1769–1772 https://halshs.archi[...] 2010-01-26
[24] 웹사이트 ランベルトの「学的認識」について : 『新オルガノン』を中心に http://repo.lib.ryuk[...]
[25] 서적 Essai d'Optique, sur la gradation de la lumière https://books.google[...] Claude Jombert 1729
[26] 서적 Photometria sive de mensura et gradibus luminis, colorum et umbrae http://imgbase-scd-u[...] Eberhardt Klett 1760
[27] PDF http://www.kuttaka.o[...]
[28] PDF http://www.kuttaka.o[...]
[29] PDF http://www.kuttaka.o[...]
[30] PDF http://www.kuttaka.o[...]
[31] PDF http://www.kuttaka.o[...]


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com